توضیحات
در علوم نظری رایانه، نظریهٔ اتوماتا (به انگلیسی: Automata theory) یا نظریهٔ ماشینها عبارت است از بررسی ریاضی ماشینهای محاسبهگر انتزاعی و تواناییهای آنها برای حل مسایل. به این ماشینهای انتزاعی اتوماتا گفته میشود. این نظریه بسیار نزدیک به نظریهٔ زبان صوری است. به طوری که اتوماتا اغلب توسط دستهٔ زبانهای رسمی قابل تشخیص دستهبندی میشوند. اتوماتا نقش اساسی در طراحی کامپایلر و تجزیه کردن (parsing) ایفا میکند. زبانهایی که توسط این ماشینها بررسی میشوند زبانهای فرمال هستند.
توضیحات پایه
یک ماشین، یک مدل ریاضی از ماشین حالات متناهی (FSM) است. یک ماشین شامل مجموعهای متناهی از حالات است که بر اساس ورودی و تابع گذار خود (که میتواند به صورت جدول باشد)، از یک حالت به حالت دیگر، تغییر وضعیت میدهد. این تابع انتقال به ماشین خودکار میگوید که به کدام حالت بعدی با توجه به حالت فعلی و نماد داده شده، برود.
به صورت کلی، یک ماشین شامل مجموعهای متناهی یا شماری از حالات مختلف است.
تعاریف پایه نظریه ماشینها
شرح غیر قرار دادی
یک ماشین خودکار قرار است که بر روی تعدادی ورودی از دنباله یا رشته در مراحل زمانی گسسته اجرا شود. در هر مرحله از زمان، ماشین یک ورودی که از مجموعهای از نمادها یا حرفها برداشته شده است را، میگیرد که به آن الفبا (Alphabet) گفته میشود. یک ماشین حاوی مجموعهٔ متناهی از حالت هاست. در هر لحظه از اجرا بسته به نوع ماشین، میتواند در یکی یا چند تا از حالت هایش باشد. در هر مرحلهٔ زمانی، هنگامی که ماشین یک نماد را میخواند، بر اساس حالت فعلی و نماد خوانده شده به حالت بعدی پرش یا گذر میکند. این تابع روی حالت فعلی و نماد ورودی تابع گذار گفته میشود. ماشین تا زمانی که یک ورودی کامل خوانده شود ورودی را نماد به نماد در دنبالهای میخواند و از حالتی به حالت دیگر بر اساس تابع گذار، گذر میکند. زمانی که ورودی نهایی خوانده میشود، اصطلاحاً ماشین متوقف شدهاست و به این حالت، حالت نهایی میگویند. بر اساس حالت نهایی گفته میشود که ماشین یک ورودی را قبول یا رد کردهاست. زیر مجموعهای از حالتهای ماشین وجود دارد که به عنوان مجموعهٔ حالتهای مورد قبول تعریف میشود. اگر حالت نهایی یک حالت مورد قبول باشد ماشین ورودی را پذیرفتهاست. در غیر این صورت ورودی رد میشود. به مجموعهای از ورودیها که توسط ماشین پذیرفته میشود زبان قابل تشخیص ماشین میگویند.
شرح قرار دادی
واژگان
- نماد: کوچکترین و بنیادیترین موجودیتی که دارای معنی یا تأثیری بر ماشین است. برخی مواقع به نمادها حرف هم گفته میشود.
- الفبا: یک مجموعه غیر تهی و متناهی از نمادها که در یک زبان تعریف شدهاند. الفبای زبان توسط Σ نشان داده میشود.
همچنین به هر نماد الفبا یک حرف گفته میشود. به عنوان مثال، الفبای لاتین {a,b،c,… ,z}=∑ و الفبای باینری {۰و۱}=∑ مثالهایی از الفبا هستند که بیشترین کاربرد را برای ما دارند.
- کلمه یا رشته: دنبالهای متناهی از نمادهای یک الفباست که با عمل الحاق به هم پیوستهاند. به عنوان مثال english یک رشته روی الفبای زبان انگلیسی است. یک مثال از رشته به صورت مقابل است: w=aabc
طول رشته با علامت |w| نمایش داده میشود و به تعداد نمادهای موجود در رشته گفته میشود. رشتهٔ تهی با نماد ε یا ℷ نمایش داده میشود و طول آن برابر صفر در نظر گرفته میشود. به عنوان مثال اگر w=abcc آنگاه: ۴=|w|
- زبان: مجموعهای از رشتهها است. این مجموعه میتواند متناهی یا نامتناهی باشد.
تعریف قراردادی
۵ تایی 
- Q مجموعهای از وضعیت هاست.
- ∑ یک مجموعهٔ کراندار از نشانه هاست که ما آن را الفبای زبانی که ماشین خودکار میپذیرد می نامیم.
- δ تابع گذار است که
- (برای ماشین خودکار غیر قطعی، یک رشتهٔ خالی نیز یک ورودی قابل قبول است)
وضعیت شروع است، یعنی وضعیتی از ماشین خودکار که در آن وضعیت، هیچیک از ورودیها هنوز پردازش نشده است. (بدیهی است که
)
مجموعهای از حالات
است (برای مثال F⊆Q) که وضعیتهای قبول نامیده میشوند.
با داشتن حرف ورودی 




با داشتن یک جفت از حروف 





این ساختار میتواند معکوس هم بشود، با داشتن 

سه تایی 

زبان پذیرفته شدهٔ ماشین خودکار (یعنی 



وقتی مجموعهٔ وضعیتهای Q کراندار است، ماشین خودکار به عنوان ماشین خودکار کراندار شناخته میشود و مجموعهٔ همهٔ زبانهای قابل تشخیص آن را، زبانهای باقاعده مینامیم. در واقع یک همارزی قوی وجود دارد: به ازای هر زبان باقاعده یک ماشین خودکار وضعیت محدود وجود دارد.
انواع ماشینهای خودکار کراندار
در زیر، سه نوع از ماشینهای خودکار کراندار ذکر شده است
- ماشینهای خودکار کراندار قطعی
- هر وضعیت از یک ماشین خودکار از این نوع، یک گذار برای هر نشانه دارد.
- ماشینهای خودکار کراندار غیر قطعی
- وضعیتهای یک ماشین خودکار کراندار غیر قطعی، ممکن است برای هر نشانه یک گذار داشته باشد و یا اصلاً انتقالی نداشته باشد و یا حتی میتواند برای یک نشانه، گذارهای متعددی داشته باشد. این ماشین خودکار، کلمه را در صورتی میپذیرد که حداقل یک مسیر از
به وضعیتی از
وجود داشته باشد. اگر گذار تعریف نشده باشد، ماشین نمیداند که چگونه به خواندن ورودی ادامه دهد و در نتیجه کلمه پذیرفته نمیشود.
- ماشینهای خودکار کراندار غیر قطعی با ε-گذار
- علاوه بر اینکه میتوانند با هر نشانهای به وضعیتهای بیشتری (یا هیچ وضعیتی) پرش کنند، این ماشینها میتوانند که به روی هیچ نشانهای پرش نکنند. به این معنا که، اگر یک وضعیت گذارهای نامگذاری شده با ε را دارد، این ماشین میتواند در هر وضعیتی که به وسیلهٔ ε-گذار بدست آمده قرار گیرد که این کار میتواند با واسطه یا بدون واسطهٔ وضعیتهای دیگر صورت گیرد. مجموعهٔ وضعیتهایی که میتوان به وسیلهٔ این شیوه از وضعیت
بدست آورد، ε-بستار برای q نامیده میشود.
با این وجود میتوان نشان داد که تمام این ماشینها، میتوانند زبانهای مشابهی را بپذیرند.
فهرست مطالب:
فصل اول: ریاضیات مقدماتی
مفاهیم نمادگذاری و مفهوم تابع
نظریه مجموعه ها
مفهوم استقراء ریاضی
گراف و انواع آن
فصل دوم: زبان ها
مفاهیم رشته و زبان
مشخصات زبان ها
مجموعه های با قاعده
فصل سوم: گرامرهای مستقل از متن
گرامرها و زبان های مستقل از متن
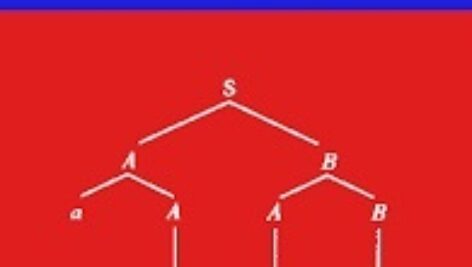
اشتقاق و درخت آن
گرامرهای قاعده
فصل چهارم: مقدمه ای بر پارسرها
اشتقاق چپ و ابهام
گراف یک گرامر
پارسر ها
فصل پنجم: فرم های نرمال
فرم های نرمال
حذف قوانین لامبدا
حذف قوانین زنجیره ای
فرم نرمال شومسکی وگریباش
فصل ششم: آتاماتی متناهی
آتاماتای قطعی
دیاگرام حالت
آتاماتای غیر قطعی
فصل هفتم: زبان ها و مجموعه های با قاعده
آتاماتای متناهی و مجموعه های با قاعده
گراف عبارت
زبان بی قاعده
فصل هشتم: آتاماتی Pushdown
آتاماتای Pushdown
انواع PDA
آتاماتای دو پشته ای
بهینه سازی DFA
فصل نهم: ماشین های تورینگ
ماشین تورینگ
انواع پذیرش
ماشین های چند شیاره
ماشین های تورینگ غیر قطعی
فصل دهم: طبقه بندی شومسکی
گرامرهای بدون محدودیت
گرامرهای وابسته به متن
آتاماتای خطی محدود
طبقه بندی شومسکی
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
 مرجع دانلود فایل | مرجع دانلود فایل
مرجع دانلود فایل | مرجع دانلود فایل









هنوز هیچ نقد و بررسی وجود ندارد.