مرجع دانلود فایل | مرجع دانلود فایل
توضیحات
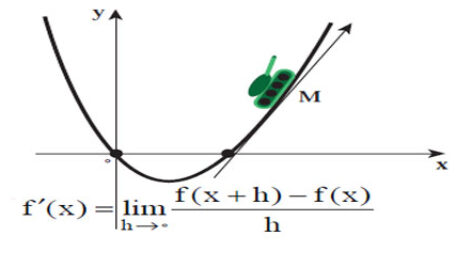
مشتق ایدهٔ اصلی حساب دیفرانسیل، بخش اول آنالیز ریاضی است که نرخ لحظه‌ای (یا نقطه‌ای) تغییرات تابع را نشان می‌دهد. مشتق نیز، نظیر انتگرال، از مسئله‌ای در هندسه، یعنی یافتن خط مماس در یک نقطه از منحنی ناشی شده‌است.
مفهوم مشتق تا اوائل قرن ۱۷ میلادی، یعنی تا قبل از آنکه ریاضی‌دان فرانسوی، پییر دو فرما به تعیین اکسترمم‌های چند تابع خاص دست بزند، تنظیم نشده بود. فرما دریافت که خطوط مماس، در نقاطی که منحنی ماکزیمم یا مینیمم دارد، باید افقی باشد. از اینرو به نظرش رسید که مسئلهٔ تعیین نقاطاکسترمم تابع، به حل مسئلهٔ دیگر، یعنی یافتن مماس‌های افقی مربوط می‌شود، تلاش برای حل این مسئلهٔ کلی‌تر بود که فرما را به کشف برخی از ایده‌های مقدماتی مفهوم مشتق هدایت کرد.
در نگاه نخست اینطور به نظر می‌رسید که بین مسئلهٔ یافتن مساحت سطح زیر یک نمودار و موضوع تعیین خط مماس بر منحنی در یک نقطه رابطه‌ای وجود ندارد، اما اولین کسی که دریافت این دو مفهومِ به ظاهر دور از هم، در واقع ارتباط نسبتاً نزدیکی با هم دارند آیزاک بارو معلم آیزاک نیوتون بوده‌است.
اما مفهوم مشتق به شکل امروزی آن، نخستین بار در سال ۱۶۶۶ میلادی توسط نیوتون و به فاصلهٔ چند سال بعد از او، توسط گوتفرید لایب نیتس، مستقل از یکدیگر پدید آمد. این دو دانشمند در ادامهٔ کار خود، باز هم به طور مستقل، بخش دوم آنالیز ریاضی یعنی حساب انتگرال را عرضه کردند که اساس آن بر عمل انتگرال‌گیری قرار دارد.
نیوتون از شیوهٔ استدلال سینماتیک و با دیدگاه فیزیکی به بررسی مشتق پرداخته و از آن برای بدست آوردن سرعت لحظه‌ای استفاده می‌کرد. اما لایب نیتس با دیدگاهی هندسی، از مشتق برای بدست آوردن ضریب زاویهٔ مماس در منحنی‌ها استفاده می‌کرد. هر یک از این دو دانشمند نمادهای جداگانه‌ای را برای نشان دادن مشتق به کار می‌بردند.
پیشرفت حساب دیفرانسیل و انتگرال در دوران بعد به آگوستین لویی کوشی، برنارد ریمان و برادران برنولی، یعنی ژاکوب و یوهان، مربوط می‌شود. گیوم لوپیتال (به فرانسوی: Guillaume de lHôpital)، دانشمند فرانسوی، در سال ۱۶۹۶ نخستین کتاب درسی مربوط به آنالیز ریاضی را با نام «آنالیز بی‌نهایت کوچک‌ها برای بررسی منحنی‌ها» منتشر کرد که در واقع خلاصه‌ای از درس‌هایی بود که یوهان برنولی به عنوان معلم برای او نوشته بود. در این کتاب، قاعدهٔ رفع ابهام در حد، با استفاده از مشتق نیز آمده که به قاعدهٔ هوپیتال مشهور است ولی در واقع متعلق به یوهان برنولی بوده‌است.
فهرست مطالب:
تعریف مشتق
نمو تابع
نماد لایبنیتز
محاسبه مشتق توابع با استفاده از تعريف
تعبیر هندسی مشتق
قضیه
خط مماس
خط قائم
مشتق تابع مرکب
قانون زنجیری
جبر مشتقات
مشتق خارج قسمت
مشتقات توابع معكوس
مشتقات مراتب بالاتر
مشتق مرتبه nام
مشتق توابع مثلثاتی
تعبير هندسي نسبت‌هاي مثلثاتي
دایره مثلثاتی
علامت توابع مثلثاتي در ناحيه‌هاي مختلف
قضیه
توابع مثلثاتي و معكوس آنها
تابع متناوب
تابع سينوس و معكوس آن
تابع كسينوس و معكوس آن
تابع تانژانت و معكوس آن
تابع كوتانژانت و معكوس آن
مشتق توابع معكوس مثلثاتي
توابع نمايي، لگاريتمي و مشتق آنها
لگاریتم طبیعی
اهم فرمول‌هاي لگاريتم
كاربرد توابع نمايي در اقتصاد و بازرگاني
توابع هذلولي و مشتق آنها
روابط بين توابع مثلثاتي هذلولي
توابع معكوس هذلولي و مشتق آنها
دیفرانسیل
دیفرانسیل تابع مرکب
جبر دیفرانسیل ها
ديفرانسيل مرتبه nام
محاسبات تقريبي به كمك ديفرانسيل
کاربردهای مشتق
جهت تغییرات تابع
ماكزيمم و مينيمم يك تابع
شرط لازم ماكزيمم و مينيمم نسبي
قضیه رول
تعبير هندسي قضيه رول
قضیه مقدار میانگین برای مشتق
تحدب و تقعر يك منحني و نقطه عطف
و…
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
هنوز هیچ نقد و بررسی وجود ندارد.