توضیحات
معادله دیفرانسیل یکی از معادله های ریاضی است و بیانگر یک تابع مجهول از یک یا چند متغیر مستقل و مشتقهای مرتبههای مختلف آن نسبت به متغیرهای مستقل است. بسیاری از قوانین عمومی طبیعت (در فیزیک، شیمی، زیستشناسی و ستارهشناسی) طبیعیترین بیان ریاضی خود را در زبان معادلات دیفرانسیل مییابند. کاربردهای معادلات دیفرانسیل همچنین در ریاضیات، بویژه در هندسه و نیز در مهندسی و بسیاری از حوزه های دیگر کاربردی و فنی فراوان هستند.
معادلات دیفرانسیل در بسیاری پدیدههای علوم رخ می دهند. هر زمان که یک رابطه بین چند متغیر با مقادیر مختلف در حالتها یا زمانهای مختلف وجود دارد و نرخ تغییرات متغیرها در زمانهای مختلف یا حالات مختلف شناخته شده است میتوان آن پدیده را با معادلات دیفرانسیل بیان کرد.
به عنوان مثال در مکانیک، حرکت جسم بوسیله سرعت و مکان آن در زمانهای مختلف توصیف میشود و معادلات نیوتن به ما رابطه بین مکان و سرعت و شتاب و نیروهای گوناگون وارده بر جسم را میدهد. در چنین شرایطی می توانیم حرکت جسم را در قالب یک معادله دیفرانسیل که در آن مکان ناشناخته جسم تابعی از زمان است بیان کنیم.
شاخه بندی
متدهای حل معادلات دیفرانسیل بسیار مرتبط با نوع معادله هستند. معادلات دیفرانسیل را به طور کلی به دو دسته می توان تقسیم کرد.
معادلات دیفرانسیل معمولی: در این نوع معادلات تابع جواب دارای تنها یک متغیر مستقل است.
معادلات دیفرانسیل با مشتقات پارهای: در این نوع معادلات تابع جواب دارای چندین متغیر مستقل میباشد.
هر دو نوع این معادلات را می توان از دیدگاه خطی یا غیر خطی بودن تابع جواب هم دسته بندی کرد. همچنین مرتبه معادلات دیفرانسیل معمولی و مشتقات پاره ای را می توان به صورت کسری در نظر گرفت که به معادلات دیفرانسیل کسری مشهورند. این نوع از معادلات دیفرانسیل نیز روش های حل گوناگونی دارند که می توان به روش تجزیه آدومیان، هوموتوپی و تکرار تغییرات اشاره نمود.
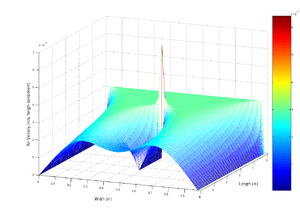
مجسم سازی جریان هوا به داخل لوله که با معادلات ناویر-استوکس، مدل سازی شدهاست، مجموعهای از معادلات دیفرانسیل جزئی
روشهای حل معادلات
به طور کل معادلات دیفرانسیل به سه روش تحلیلی، نیمه تحلیلی و عددی حل میشوند. برخی از معادلات دارای جواب دقیق و فرم تابعی هستند اینگونه معادلات را میتوان از روشهای تحلیلی حل نمود و به جواب دقیق رسید. معادلات دیگر که دارای فرم تابع مشخص نیستند را بایستی توسط روشهای نیمه تحلیلی یا عددی حل کرد. از روشهای نیمه تحلیلی میتوان به روش تجزیه آدومیان، آنالیز هموتوپی، تبدیل دیفرانسیل و… اشاره کرد. روشهای عددی دامنه وسیع تری را برای حل معادلات به کار میگیرد. از روشهای عددی میتوان به روش اویلر، روش هون، روش تیلور، روش رانگ-کوتا، آدامز-بشفورث-مولتون، روش میلن سیمپسون، روش هامینگ، روش رانگ-کوتا فلبرگ مرتبه ۵، روش رحمانزاده کای وایت، روشهای طیفی و شبه طیفی، روشهای شبکهای همانند اجزای محدود و تفاضل محدود و روشهای بدون شبکه اشاره کرد .
فهرست مطالب:
فصل اول: معادلات دیفرانسیل مرتبه اول
مقدمه
مرتبه و درجه معادله دیفرانسیل
معادله دیفرانسیل جداشدنی
معادله دیفرانسیل همگن
دسته منحنی ها و دسته منحنی های متعامد
معادله دیفرانسیل کامل
عامل انتگرال ساز
معادله دیفرانسیل مرتبه اول خطی
معادله برنولی
معادله کلرو
معادله ریکاتی
و…
فصل دوم: معادلات دیفرانسیل مرتبه دوم و مراتب بالاتر
معادله مرتبه دوم حالت خاص فاقد y یا x
معادلات قابل تبدیل به مرتبه اول
معادلات با ضرایب ثابت همگن
رونسکین
معادله کوشی-اویلر
معادله دیفرانسیل مرتبه دوم خطی غیر همگن
روش تغییر پارامتر
روش ضرایب ثابت
و…
فصل سوم: حل معادله دیفرانسیل به روش سری ها
مقدمه
سری توانی
بسط مک لورن
نقاط معمولی و منفرد
جواب های سری معادلات دیفرانسیل
روابط بازگشتی
نقاط منفرد منظم معادلات دیفرانسیل خطی مرتبه دوم
روش فروبنیوس
بررسی حالت کلی معادله دیفرانسیل مرتبه دوم
و…
فصل چهارم: دستگاه معادلات دیفرانسیل
تعریف
روش های حل
روش اول: یكی از معادلات دستگاه مستقلاً قابل حل می باشد
روش دوم: حل دستگاه دو معادله مرتبه اول خطی با ضرایب ثابت
روش سوم: این روش مشهور به روش عملگر یا اپراتور می باشد
و…
فصل پنجم: تبدیل لاپلاس
مفهوم تبدیل لاپلاس
تعریف
خواص تبدیل لاپلاس
معكوس تبدیل لاپلاس
خواص معكوس تبدیل لاپلاس
حل معادله دیفرانسیل به روش لاپلاس
تبدیل لاپلاس برخی توابع
و…
به همراه مثال های حل شده فراوان در هر فصل.
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
 مرجع دانلود فایل | مرجع دانلود فایل
مرجع دانلود فایل | مرجع دانلود فایل


هنوز هیچ نقد و بررسی وجود ندارد.