پاورپوینت کامل و جامع با عنوان توابع بسل در 57 اسلاید
تعداد بازدید
60 بازدید
تومان30.200

توضیحات

توابع بسل، (به انگلیسی: Bessel functions) اولین بار توسط دانیل برنولی تعریف شدند و سپس فردریش بسل فرم عمومی آن را بررسی نمود. توابع بسل جواب‌های معادله دیفرانسیل زیر می‌باشند:

{displaystyle x^{2}{frac {d^{2}y}{dx^{2}}}+x{frac {dy}{dx}}+(x^{2}-alpha ^{2})y=0}

معادله بسل معادله‌ای است که از معادلات قابل حل با سری‌هاست، و دارای نقطه تکین منظم است. نقطه x=0 تنها نقطه غیرعادی معادله فوق است. جواب‌های معادله به توابع بسل معروفند. در معادلهٔ بالا{displaystyle alpha } یک عدد حقیقی یا یک عدد مختلط دلخواه می‌باشد که مرتبه تابع بسل را مشخص می‌کند.

بطورکلی توابع بسل از حل معادلات دیفرانسیل پاره‌ای لاپلاس و معادله هلمهولتز در مختصات استوانه‌ای و مختصات کروی بدست می‌آیند. از این رو این توابع در تئوری انتشار امواج و تئوری پتانسیل اهمیت بسزایی دارند. البته این توابع در حل معادلات ارتعاشات، معادلات رسانایی گرما و امواج الکترومغناطیس در مختصات استوانه‌ای ظاهر می‌شوند.

تعریف

توابع بسل نوع اول آن دسته توابعی هستند که مربوط به {displaystyle alpha } بعنوان عدد طبیعی منفی می‌باشند که در صفر متناهی می‌باشد:

{displaystyle J_{alpha }(x)=sum _{m=0}^{infty }{frac {(-1)^{m}}{m!Gamma (m+alpha +1)}}{left({frac {x}{2}} ight)}^{2m+alpha }}

که{displaystyle Gamma (z)} تابع گاما می‌باشد که حالت کلی فاکتوریل برای اعداد غیرطبیعی می‌باشد.

 

نمودار توابع بسل از نوع اول، Jα(x)، به ازای مقادیر صحیح مرتبه α=0,1,2.

 

توابع بسل نوع دوم آن دسته توابعی هستند که در مبدا مختصات (نقطه صفر) تکین (Singular) هستند:

{displaystyle Y_{alpha }(x)={frac {J_{alpha }(x)cos(alpha pi )-J_{-alpha }(x)}{sin(alpha pi )}}}

 

فهرست مطالب:

تابع مولد

بسط سری

مرتبه درست منفی

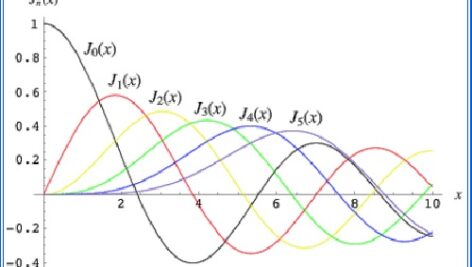
نمودار

روابط بازگشتی

معادله دیفرانسیل بسل

نمایش انتگرالی

حالت خاص

پرش فرانهوفر

کاواک مشدد استوانه ای

شرایط مرزی

صفرهای توابع بسل

رهیافتها به توابع بسل

تعامد

سری بسل

پتانسیل الکتروستاتیکی در استوانه توخالی

تابع نویمن

فرمولهای رونسکی

موجبرهای هم محور مغناطیسی عرضی

توابع هنکل

امواج پیشرونده استوانه ای

انتگرال اشلافلی

توابع بسل و نویمن بر حسب توابع هنکل

معادله هلم هولتز

توابع تعدیل یافته بسل

تابع تعدیل یافته بسل نوع دوم

تابع تعدیل یافته بسل نوع اول

یک نمایش انتگرالی برای تابع تعدیل یافته نوع دوم

بسط مجانبی تابع تعدیل یافته نوع دوم

و…

راهنمای خرید:
  • لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
  • همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
  • ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
  • در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
نقد و بررسی‌ها

هنوز هیچ نقد و بررسی وجود ندارد.

اضافه کردن نقد و بررسی

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *