توضیحات
دستگاه مختصات دکارتی، در هندسه، به نمایش هر نقطه از صفحه با دو عدد (یک زوج مرتب) گفته میشود. این دو عدد را معمولاً به نامهای مختصه X و مختصه Y میخوانند. در دستگاه محورهای مختصات دوبعدی، محورهای zو Y برهم عمودند، از همین رو این دستگاه را دستگاه محورهای متعامد نیز میگویند.
برای نمایش هندسی هر نقطه، دو خط عمود برهم را، که محور مختصات X (خُفت یا آبسیس) و محور مختصات Y، (یا رُست) نامیده میشوند، رسم میکنند و از محل تقاطع این دو محور، که مبدأ مختصات نام دارد، روی هر محور به اندازه مختصه X و مختصه Y دو طول را (بر حسب واحد طول) مشخص میکنند. خطهایی که در انتهای این طولها عمود بر محورهای مختصات رسم شود در نقطهای یکدیگر را قطع میکنند. این محل تقاطع نمایش هندسی نقطه مورد نظر است.
نام این دستگاه مختصات از نام ریاضیدان و فیلسوف فرانسوی رنه دکارت (۱۵۹۶-۱۶۵۰) که این روش را برای مشخص کردن یک نقطه در صفحه کشف کرد، گرفته شدهاست.
با کاربرد دستگاه مختصات دکارتی امکان رسم معادلات جبری به صورت خط و منحنی یا محاسبه زوایا و فواصل و همچنین نوشتن معادله مختصات یک شکل در صفحه فراهم میشود.
دستگاه مختصات قطبی، یک دستگاه مختصات دوبعدی است که در آن مکان هر نقطه، با فاصلهٔ آن تا مرکز مختصات (r) و زاویه بین خط رسمشده از مرکز به آن نقطه و محور طول (θ) مشخص میشود. این دستگاه در سه بعد به دستگاه مختصات استوانهای و دستگاه مختصات کروی تبدیل میشود.
اولین استفادههای مشابه که به ایجاد کنونی این دستگاه انجامیدهاست توسط ابوریحان بیرونی انجام شد.
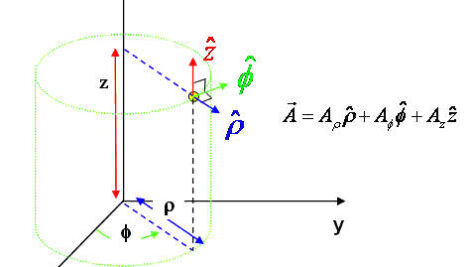
مختصات استوانهای نوعی مختصات متعامد (عمود برهم) است که در آن یک نقطه، در فضا بر روی قاعدهٔ یک استوانه در نظر گرفته میشود. مکان آن نقطه بر اساس شعاع و ارتفاع استوانه (r و z) و زاویهای که شعاع قاعده گذرنده از آن نقطه با محور x میسازد (θ)، بیان میشود. این دستگاه، در حالت دوبعدی، با حذف مختص z به مختصات قطبی تبدیل میشود. در فیزیک و به ویژه در مباحث الکترومغناطیس و مخابرات به جای r، θ،z به ترتیب از حروف ρ، φ،z استفاده میشود.
دستگاه مختصات کروی، دستگاه مختصاتی با سه مختصهاست:
- مختصه
(یا
) که روی کرههای هم مرکز حول مبدأ است.
- مختصه
روی مخروطهای دوار قائم حول محور
با راس واقع در مبدأ.
- مختصه
که روی نیم صفحاتی که از محور قطبی
میگذرد.
در فیزیک بنا به سنت جای 



فهرست مطالب:
مقدمه
مختصات خمیده خط
بردار دلخواه در مختصات خمیده خط
اگر دستگاه مختصات خمیده متعامد باشد
به دست آوردن عامل مقیاس
مجذور عنصر فاصله در مختصات خمیده خط
شرایط متعامد بودن یک دستگاه مختصات
بردار دیفرانسیلی فاصله
عنصرسطح در مختصات خمیده خط
عنصر حجم در مختصات خمیده خط
دستگاه های مختصات خاص
دستگاه مختصات کروی
روابط تبدیل بین دستگاه های مختصات کروی و دکارتی
بردارهای یکه مختصات کروی برحسب بردارهای یکه مختصات دکارتی
عامل های مقیاس در مختصات کروی
عنصر حجم در مختصات کروی
عنص رسطحی در مختصات کروی
عنصر زاویه حجمی
گرادیان (شیب تابع) در مختصات کروی
واگرایی (دیوژرانس) در مختصات کروی
لاپلاسین در مختصات کروی
تاو (کرل) بردار در مختصات کروی
دستگاه مختصات استوانه دوار
روابط تبدیل بین دستگاه مختصات استوانه ای و دکارتی
عامل های مقیاس در مختصات استوانه ای
عنصر حجم در مختصات استوانه ای
بردارهای یکه مختصات استوانه ای بر حسب بردارهای یکه مختصات دکارتی
گرادیان (شیب تابع) در مختصات استوانه ای
واگرایی (دیوژرانس) در مختصات استوانه ای
لاپلاسین در مختصات استوانه ای
تاو (کرل) بردار در مختصات استوانه ای
حل معادله های دیفرانسیل جزیی در دستگاه های مختلف
جداسازی متغیرها
جداسازی متغیرها در دستگاه مختصات دکارتی
جداسازی متغیرها در دستگاه مختصات استوانه ای دوار
معادله بسل
جداسازی متغیرها در دستگاه مختصات قطبی کروی
معادله رسانش گرما یا پخش نوترون
معادله هلمهولتز
معادله موج
و…
به همراه بیش از 70 مثال و تمرین حل شده از مباحث مختلف.
- لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
- همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
- ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
- در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.
 مرجع دانلود فایل | مرجع دانلود فایل
مرجع دانلود فایل | مرجع دانلود فایل


هنوز هیچ نقد و بررسی وجود ندارد.