Name: پاورپوینت کامل و جامع با عنوان آنالیز برداری (کرل، گرادیان، دیورژانس، مشتق و انتگرال و...) در 120 اسلاید
Availability: InStock

توضیحات

آنالیز برداری در مقابل آنالیز اسکالر قرار می گیرد.

در حالت برداری علاوه بر اندازه، جهت نیز اهمیت دارد و به همین دلیل است که به آن برداری می گویند. در این نوع آنالیز مشابه حالت نرده‌ای آن عملیات های اصلی شامل جمع، تفریق، ضربو تقسیم تعریف می شود که ضرب خود به دو گونهٔ ضرب داخلی و خارجی دسته بندی می شود.

در حسابان بردارها شیو یا گرادیان یک میدان نرده‌ای، میدانی برداری است که مؤلفه‌های آن نرخ تغییر میدان نخستین را در جهت‌های مختلف نشان می‌دهد. جهت خود میدان برداری گرادیان جهت بیشینهٔ تغییرات است.

به تعبیر دیگر برداری که اندازه و جهت حداکثر نرخ فضائی تغییر یک کمیت عددی را نمایش می دهد، گرادیان آن کمیت عددی تعریف می کنیم. $abla f = left(frac{partial f}{partial x_1 }, dots, frac{partial f}{partial x_n } ight)$

در حالت خاص برای اسکالر ‎‎، گرادیان f در دستگاه کارتزین به صورت زیر نوشته می‌شود:

اگر x و y و z سه مختصه دستگاه مختصات دکارتی باشند، دیورژانس بردار ‎ F(x,y,z) = F_x i + F_y j + F_z k ‏ در مختصات دکارتی به صورت زیر تعریف می‌شود: $operatorname {div},{mathbf {F}}= abla cdot {mathbf {F}}={frac {partial F_{x}}{partial x}}+{frac {partial F_{y}}{partial y}}+{frac {partial F_{z}}{partial z}}.$

که در آن ‎ F_x , F_y , F_z ‏ مولفه‌های بردار F در راستای x , y, z است.

به طور کلی در مختصات مایل داریم:

$abla cdot {mathbf {F}}={{1} over {h_{1}h_{2}h_{3}}}[{frac {partial }{partial q_{1}}}(F_{1}h_{2}h_{3})+{frac {partial }{partial q_{2}}}(F_{2}h_{3}h_{1})+{frac {partial }{partial q_{3}}}(F_{3}h_{1}h_{2})]$

چرخش یا تاو میدان برداری A که با هر یک از نمادهای ، {displaystyle {oldsymbol {
abla }}wedge mathbf {A} } ، ، {displaystyle {vec {
abla }}wedge {vec {mathrm {A} }}} ، {displaystyle {vec {
abla }} imes {vec {mathrm {A} }}} ، و یا curl A نمایش داده می شود، برداری است که اندازه آن حداکثر گردش خالص A در واحد سطح است وقتی که سطح به سوی صفر میل می‌کند و جهت آن جهت عمود سطح است زمانی که سطح طوری جهت داده شده باشدکه گردش خالص را حداکثر نماید.

یک میدان برداری بدون چرخش، میدان غیر گردشی یا میدان ذخیره شونده نامیده می شود.

اگر بردار v به صورت v(x,y,z) = v_x i + v_y j + v_z k تعریف شده باشد، چرخش v عبارت است از:

${mbox{curl}};{vec v}=left({partial v_{z} over partial y}-{partial v_{y} over partial z} ight){mathbf {i}}+left({partial v_{x} over partial z}-{partial v_{z} over partial x} ight){mathbf {j}}+left({partial v_{y} over partial x}-{partial v_{x} over partial y} ight){mathbf {k}}= abla imes {vec v}$

که معادل است با دترمینان ماتریسی که

$abla imes {vec v}=left|{egin{matrix}{mathbf {i}}&{mathbf {j}}&{mathbf {k}}\{{frac {partial }{partial x}}}&{{frac {partial }{partial y}}}&{{frac {partial }{partial z}}}\v_{x}&v_{y}&v_{z}end{matrix}} ight|.$

فهرست مطالب:

تعاریف

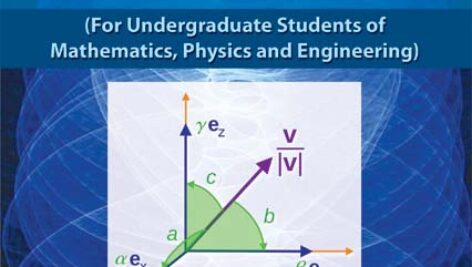
نمایش بردار در فضا

نمایش مولفه ای بردارها

کسینوس های هادی

جمع و تفریق به روش مولفه ای

ضرب داخلی

زاویه بین دو بردار

کاربردهای ضرب داخلی

ضرب برداری

قانون سینوس ها

ضرب سه گانه بردارها

قاعده بک-کب

حجم متوازی السطوح

میدان های نرده ای و برداری

گرادیان و مشتق جهتی

عملگر گرادیان در مختصات دکارتی

انتگرال برداری

انتگرال خطی یک بردار

انتگرال سطحی

انتگرال حجمی

دیورژانس یا واگرایی

دیورژانس یک تابع برداری

دیورژانس در مختصات دکارتی

قضیه واگرایی گاوس

زاویه فضایی

کرل یا تاو

کرل یک میدان برداری

کرل درمختصات دکارتی

قضیه استوکس

عملگر لاپلاسین

و…

همچنین این فایل با بیش از 70 مثال حل شده می تواند به عنوان یک مرجع آموزشی کامل برای رشته های ریاضی و فیزیک و همچنین مبحث آنالیز برداری الکترومغناطیس استفاده شود.

راهنمای خرید:

لینک دانلود فایل بلافاصله بعد از پرداخت وجه به نمایش در خواهد آمد.
همچنین لینک دانلود به ایمیل شما ارسال خواهد شد به همین دلیل ایمیل خود را به دقت وارد نمایید.
ممکن است ایمیل ارسالی به پوشه اسپم یا Bulk ایمیل شما ارسال شده باشد.
در صورتی که به هر دلیلی موفق به دانلود فایل مورد نظر نشدید با ما تماس بگیرید.

نقد و بررسی‌ها

هنوز هیچ نقد و بررسی وجود ندارد.

اضافه کردن نقد و بررسی

پاورپوینت کامل و جامع با عنوان آنالیز برداری (کرل، گرادیان، دیورژانس، مشتق و انتگرال و…) در 120 اسلاید

توضیحات

اشتراک گذاری در شبکه های اجتماعی